Bode's sensitivity integral
Bode's sensitivity integral, discovered by Hendrik Wade Bode, is a formula that quantifies some of the limitations in feedback control of linear parameter invariant systems. Let L be the loop transfer function and S be the sensitivity function.
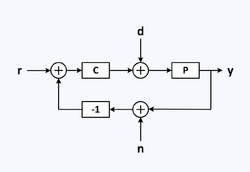
In the diagram, P is a dynamical process that has a transfer function P(s). The controller, C, has the transfer function C(s). The controller attempts to cause the process output, y, to track the reference input, r. Disturbances, d, and measurement noise, n, may cause undesired deviations of the output. Loop gain is defined by L(s) = P(s)C(s).
The following holds:
- [math]\displaystyle{ \int_0^\infty \ln |S(j \omega)| d \omega = \int_0^\infty \ln \left| \frac{1}{1+L(j \omega)} \right| d \omega = \pi \sum Re(p_k) - \frac{\pi}{2} \lim_{s\rightarrow\infty} s L(s) }[/math]
where [math]\displaystyle{ p_k }[/math] are the poles of L in the right half plane (unstable poles).
If L has at least two more poles than zeros, and has no poles in the right half plane (is stable), the equation simplifies to:
- [math]\displaystyle{ \int_0^\infty \ln |S(j \omega)| d \omega = 0 }[/math]
This equality shows that if sensitivity to disturbance is suppressed at some frequency range, it is necessarily increased at some other range. This has been called the "waterbed effect."[1]
References
Further reading
- Karl Johan Åström and Richard M. Murray. Feedback Systems: An Introduction for Scientists and Engineers. Chapter 11 - Frequency Domain Design. Princeton University Press, 2008. http://www.cds.caltech.edu/~murray/amwiki/Frequency_Domain_Design
- Stein, G. (2003). "Respect the unstable". IEEE Control Systems Magazine 23 (4): 12–25. doi:10.1109/MCS.2003.1213600. ISSN 1066-033X.
- Costa-Castelló, Ramon; Dormido, Sebastián (2015). "An interactive tool to introduce the waterbed effect". IFAC-PapersOnLine 48 (29): 259–264. doi:10.1016/j.ifacol.2015.11.246. ISSN 2405-8963.
External links
- WaterbedITOOL - Interactive software tool to analyze, learn/teach the Waterbed effect in linear control systems.
- Gunter Stein’s Bode Lecture on fundamental limitations on the achievable sensitivity function expressed by Bode's integral.
- Use of Bode's Integral Theorem (circa 1945) - NASA publication.
See also
 |